PLASTIC
Bulk Data Entry Can be used to describe elasto-plastic material behavior (currently supported for MAT1).
Format
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| PLASTIC | MID | ||||||||
| CRIT | CRITERIA | OPT1 | OPT2 | ||||||
| C | C | C | C | C | C | C7 | |||
| etc | etc | etc | etc | etc | etc | etc | |||
| HARD | HARDENING | ||||||||
| H | H | H | H | H | H | H7 | |||
| etc | etc | etc | etc | etc | etc | etc | |||
| SRATE | RATE_DEP | VPLAS | FCUT | ||||||
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | |||
| etc | etc | etc | etc | etc | etc | etc |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| CRIT | HILL | ||||||||
| R11_1 | R22_1 | R33_1 | R12_1 | R31_1 | R23_1 | TEMP_1 | |||
| R11_2 | R22_2 | R33_2 | R12_2 | R31_2 | R23_2 | TEMP_2 | |||
| etc | etc | etc | etc | etc | etc | etc |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| CRIT | HILL | CLAS | |||||||
| F_1 | G_1 | H_1 | L_1 | M_1 | N_1 | TEMP_1 | |||
| F_2 | G_2 | H_2 | L_2 | M_2 | N_2 | TEMP_2 | |||
| etc | etc | etc | etc | etc | etc | etc |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| CRIT | HILL | LANK | (DIR1/ DIR2) | ||||||
| r00_1 | r45_1 | r90_1 | TEMP_1 | ||||||
| r00_2 | r45_2 | r90_2 | TEMP_2 | ||||||
| etc | etc | etc | etc |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| HARD | ISOT | ||||||||
| YIELD_1_1 | PLAS_1_1 | TEMP_1 | |||||||
| YIELD_1_2 | PLAS_1_2 | ||||||||
| YIELD_1_3 | PLAS_1_3 | ||||||||
| YIELD_2_2 | PLAS_2_2 | TEMP_2 | |||||||
| etc | etc | etc |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| HARD | JCOOK | ||||||||
| A | B | n |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| HARD | VOCE | ||||||||
| R0 | Q1 | b1 | Q2 | b2 | Q3 | b3 |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| HARD | LINVOCE | ||||||||
| R0 | H | Q | B |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| SRATE | JCOOK | VPLAS | FCUT | ||||||
| C | EPS0 |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| SRATE | COWPER | VPLAS | FCUT | ||||||
| p | c |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| SRATE | NLINEAR | VPLAS | FCUT | ||||||
| c | EPS0 |
Example (PLASTIC)
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| MAT1 | 1 | 192400.0 | 0.3 | 7.85E-9 | |||||
| PLASTIC | 1 | ||||||||
| CRIT | HILL | CLAS | |||||||
| 0.200 | 0.300 | 0.400 | 0.350 | 0.450 | 0.550 | 0.0 | |||
| HARD | ISOT | ||||||||
| 282.5 | 0.0 | 20 | |||||||
| 294.2 | 0.0025 | ||||||||
| 305.3 | 0.005 | ||||||||
| 423.1 | 0.05 | ||||||||
| 482.3 | 0.3 | ||||||||
| SRATE | NLINEAR | VPLAS | |||||||
| 0.05 | 0.01 |
Definitions
| Field | Contents | SI Unit Example |
|---|---|---|
| MID | Elastic material identification
number (MAT1). No default (Integer > 0) |
|
| CRIT | Flag indicating that the yield criterion input data are to follow. | |
| CRITERIA | Character String representing the
chosen yield criterion.
|
|
| OPT1 | HILL criterion options:
|
|
| OPT2 | HILL criterion options with
LANK input:
No default (Integer = 1 or 2) |
|
| Ci | Yield criterion input data.
(described below for each yield criterion) Comment 2 No default (Real > 0.0) |
|
| Rij_n | Stress ratio used to compute the
Hill coefficients for shear planes. Comment 2
No default (Real > 0.0) |
|
| Rii_n | Stress ratio used to compute the
Hill coefficients for normal direction. Comment 2 No default (Real > 0.0) |
|
| TEMP_n | Temperature of the material. “n”
number of temperatures can be defined. No default (Real > 0.0) |
|
| F_n,G_n, H_n, L_n, M_n, N_n | Hill orthotropy coefficients for
“n” temperatures. Comment 2
No default (Real > 0.0) |
|
| r00_n | Lankford coefficient at 0 degrees
orientation angle for “n” temperatures. No default (Real > 0.0) |
|
| r45_n | Lankford coefficient at 45 degrees
orientation angle for “n” temperatures. No default (Real > 0.0) |
|
| r90_n | Lankford coefficient at 90 degrees
orientation angle for “n” temperatures. No default (Real > 0.0) |
|
| HARD | Flag indicating that the hardening rule input data are to follow. | |
| HARDENING | Character string represents the
chosen isotropic hardening rule.
|
|
| Hi | Isotropic work hardening rule input data (described below for each hardening keyword). | |
| YIELD_n_i | Yield stress values defined for the
yield versus plasticity curve. It can be defined for “n”
temperatures. No default (Real > 0.0) |
|
| PLASTIC_n_i | Plasticity values defined for the
yield versus plasticity curve. It can be defined for “n”
temperatures. No default (Real > 0.0) |
|
| A | Initial yield stress. No default (Real > 0.0) |
|
| B | Hardening modulus. No default (Real > 0.0) |
|
| n | Hardening exponent. No default (Real > 0.0) |
|
| R0 | Initial yield stress. No default (Real > 0.0) |
|
| Qi | Saturation moduli. No default (Real > 0.0) |
|
| bi | Hardening saturation rates. No default (Real > 0.0) |
|
| H | Linear modulus. No default (Real > 0.0) |
|
| SRATE | SRATE flag indicating that the strain rate dependency input data are to follow. | |
| RATE_DEP | Character string represents the
chosen strain rate dependency rule.
|
|
| Si | Strain rate dependency rule input data (described below for each strain rate dependency rule). | |
| VPLAS | Optional keyword to activate the full visco-plastic formulation. | |
| FCUT | Cutoff frequency in case if total
strain rate is used (when VPLAS is not
activated). No default (Integer > 0) |
|
| C | Johnson-Cook parameter. No default (Real > 0.0) |
|
| EPS0 | Reference strain rate delimiting
the transition between the inviscid domain and the strain rate
dependent domain. No default (Real > 0.0) |
|
| c | Strain rate dependency
parameter. No default (Real > 0.0) |
|
| p | Strain rate exponent
parameter. No default (Real > 0.0) |
|
| CS | Strain rate dependency
exponent. No default (Real > 0.0) |
Comments
- General elasto-plastic behavior
PLASTIC option is a modular approach that can be used to add plasticity to an existing elastic material defined through MAT1. The yield function is a basic to define an elasto-plastic constitutive model through the equation:
This function defines a criterion to reach, triggering the plastic behavior. Thus:- the behavior remains elastic,
- the criterion is fulfilled, and plasticity occurs.
From a numerical point of view, a trial value of the yield function is used to determine if the plastic return mapping is necessary. This return mapping procedure takes place when , and finish after several iterations until the yield function is brought back to a zero value. The default algorithm is the cutting plane method.
The yield function is composed of two major components:- The equivalent stress denoted defines the shape of the yield surface in the stress state reference system. In other words, it corresponds to the yield criterion. Its computation depends on the stress tensor.
- The yield stress denoted defines the evolution of the yield surface size (increase/decrease) considering a combination of nonlinear phenomena: work hardening, visco-plasticity, etc. Thus, its computation may depend on several internal variables: plastic strain, plastic strain rate and even temperature.
PLASTIC then offers the possibility to create a specific assembly of constitutive equations choosing a custom-made combination of yield criterion, hardening rule, and/or strain rate dependency, among an existing library.
- Yield criterion
The CRIT continuation line is used to define the yield criterion. Currently, only HILL criterion is supported. This criterion defines a surface in the stress state reference system that triggers the beginning of plastic behavior. Its shape is defined through the equation of the equivalent stress denoted as .
Hill 1948 (HILL):
The Hill yield criterion (1948) is an orthotropic version of the quadratic yield criterion which is described as:
The equivalent stress for Hill yield criterion is obtained with:
For shell elements, the plane stress assumption implies the following equivalent stress:
Where, are the Hill orthotropy coefficients.
Some examples of the presented criterion shapes are given in Figure 1.Figure 1. Examples of Hill criterion shapes 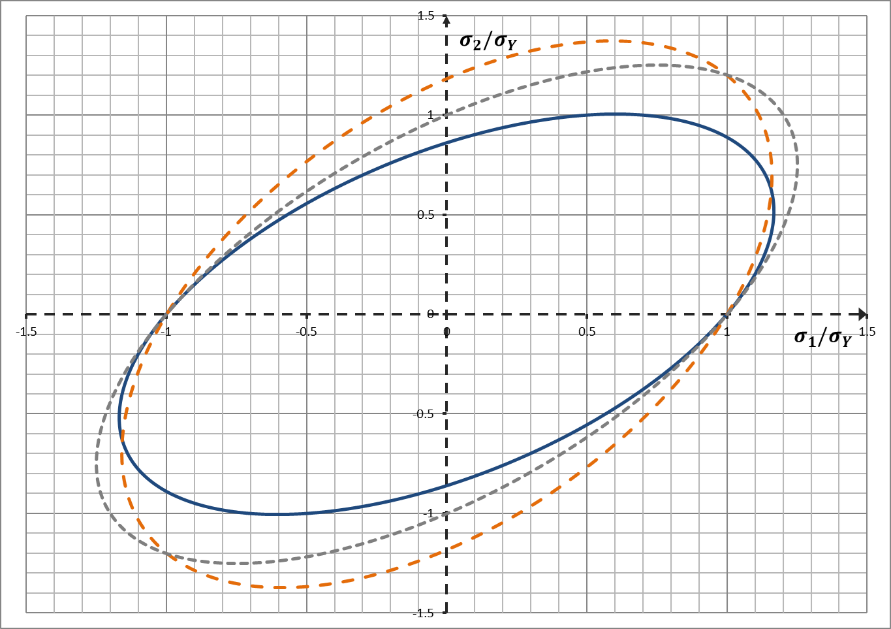
- The default input
format of Hill criterion parameters describes a list of stress
ratios which allows to compute the Hill coefficients as:Where,
- is for normal directions
- is for shear planes
Note: is the initial elastic limit stress measured for the direction .These stress ratios can be input as:(1) (2) (3) (4) (5) (6) (7) (8) (9) (10) CRIT HILL R11_1 R22_1 R33_1 R12_1 R31_1 R23_1 TEMP_1 R11_2 R22_2 R33_2 R12_2 R31_2 R23_2 TEMP_2 etc etc etc etc etc etc etc A series of several lines of stress ratios can be defined for “n” specific temperature values (TEMP_n). If several lines are defined, the stress ratios are interpolated according to the current element temperature value.
- Another input format is
available by using the keyword CLAS, for the
classical Hill shape input. This allows to directly input the Hill
coefficients instead of the stress ratios:
(1) (2) (3) (4) (5) (6) (7) (8) (9) (10) CRIT HILL CLAS F_1 G_1 H_1 L_1 M_1 N_1 TEMP_1 F_2 G_2 H_2 L_2 M_2 N_2 TEMP_2 etc etc etc etc etc etc etc - The last input format
is particularly useful when orthotropic sheets of material are
considered (and thus, plane stress conditions). It allows the user
to define the Lankford coefficient, considering the corresponding
Hill criterion formula:
Where, and .
This additional input format can be activated when using the optional keyword LANK.(1) (2) (3) (4) (5) (6) (7) (8) (9) (10) CRIT HILL LANK (DIR1/ DIR2) r00_1 r45_1 r90_1 TEMP_1 r00_2 r45_2 r90_2 TEMP_2 etc etc etc etc Another keyword can be combined with LANK, allowing to select the reference direction for which the yield stress has been measured. Orthotropic directions 1 and 2 can be selected using respectively the keywords DIR1 or DIR2. If a keyword is not used, an average yield stress is considered by default.
- The default input
format of Hill criterion parameters describes a list of stress
ratios which allows to compute the Hill coefficients as:
- Isotropic hardening rule When the equivalent stress is chosen representing the yield criterion, the other part of the elasto-plastic model, that is, the yield stress , must be defined accounting for one or several nonlinear phenomena: work hardening, visco-plasticity, etc. The first and most essential nonlinear phenomenon that can be defined is the hardening rule. This defines the increase of the yield stress following the increase of plasticity and is denoted .
- Tabulated
(ISOT) You can choose to directly input a curve to describe the increase of the yield stress with plasticity. The yield stress evolution should be either increasing monotonically or saturating to a constant value. A direct tabulated input format is thus available in the hardening rule definition.
(1) (2) (3) (4) (5) (6) (7) (8) (9) (10) HARD ISOT YIELD_1_1 PLAS_1_1 TEMP_1 YIELD_1_2 PLAS_1_2 YIELD_1_3 PLAS_1_3 YIELD_2_2 PLAS_2_2 TEMP_2 etc etc etc - Johnson-Cook
(JCOOK)
The classical power law proposed by Johnson-Cook is available in PLASTIC Bulk Data Entry. This allows to describe the following hardening rule.
Where,- Initial yield stress
- Hardening modulus
- Hardening exponent
Figure 2. Johnson-Cook hardening rule shape example 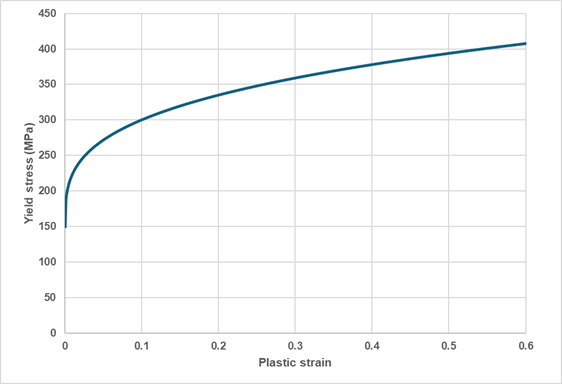
- Voce 3 terms
(VOCE)
Saturation work hardening law can also be used in PLASTIC with Voce formula, restricted to a maximum of 3 exponential terms in OptiStruct. It is described with:
Where,- Initial yield stress
- Saturation moduli
- Hardening saturation rates
Note: When , the yield stress reaches a saturation value which equals to:Figure 3. Voce 3 terms hardening rule shape example 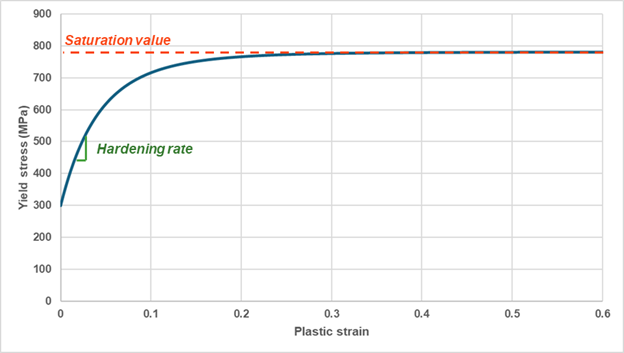
- Linear/Voce
combination (LINVOC)
With PLASTIC it is also possible to combine the effect of linear hardening and saturation Voce law allowing to control the slope of the yield stress increase after saturation. This is available with the keyword LINVOC which describes the following hardening rule:
Where,- Initial yield stress
- Linear modulus
- Saturation moduli
- Hardening rate parameter
Figure 4. Linear-Voce hardening rule shape example 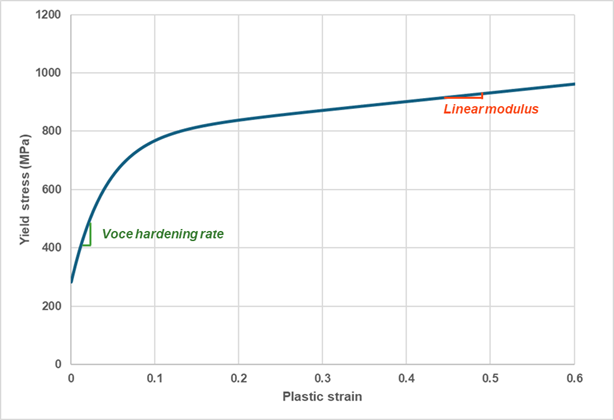
- Tabulated
(ISOT)
- Strain rate dependency rule
In addition to work hardening, you may want to introduce a strain rate dependency. This allows to increase or decrease the yield stress depending on either the total strain rate (that may be filtered using the real value parameter FCUT), or the plastic strain rate (which corresponds to a full viscoplastic formulation activated by the keyword VPLAS).
- Johnson-Cook
(JCOOK)
The Johnson-Cook strain rate dependency is a well-known solution to add strain rate dependency to an elasto-plastic behavior. The hardening rule is then multiplied by:
Where,- Johnson-Cook parameter
- Reference strain rate delimiting the transition between the inviscid domain and the strain rate dependent domain
The Johnson-Cook model thus describes a linear increase of the material strength with respect to the logarithm of the strain rate. (Figure 5). An example of yield stress increase shape obtained with the presented model is given in Figure 6.Figure 5. Johnson-Cook strain rate dependency model
Figure 6. Johnson-Cook stress rate dependency model 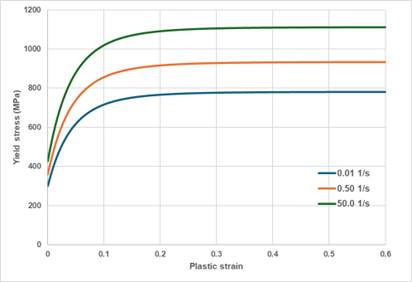
- Cowper-Symonds
(COWPER)
The Cowper-Symonds rate dependency is another solution commonly found in the literature. It modifies the yield stress equation a:
Where,- Strain rate dependency parameter
- Strain rate exponent parameter
The shape of the presented model is given in Figure 7.Figure 7. Cowper-Symonds strain rate dependency model 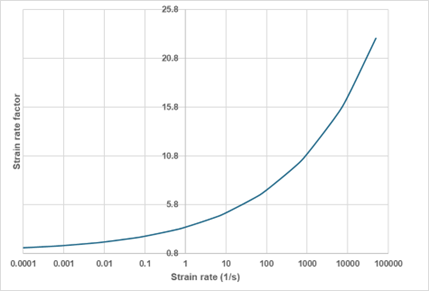
Figure 8. Cowper-Symonds stress rate dependency model 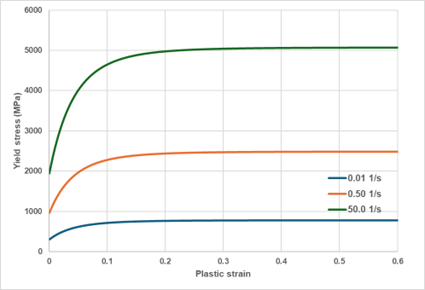
- Nonlinear
(NLINEAR)
The nonlinear strain rate dependency is similar to the Johnson-Cook model described above. Nevertheless, it describes a nonlinear evolution of the strain rate dependency in the logarithmic scale (Figure 9). This is introduced in the yield stress formula as:
Where,- Strain rate dependency exponent
- Reference strain rate delimiting the transition between the inviscid domain and the strain rate dependent domain
An example of the presented model on the yield stress shape is given in Figure 10.Figure 9. Nonlinear strain rate dependency model
Figure 10. Nonlinear stress rate dependency model 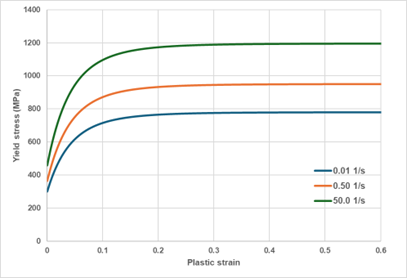
- Johnson-Cook
(JCOOK)
- The model obtained with this
example has an isotropic elastic behavior, with an orthotropic
elasto-plasticity using a HILL yield criterion, and a
specific yield stress assembly cumulating:
- A tabulated work hardening,
- A nonlinear strain rate dependency with full visco-plastic formulation
Note: Failure can be added to the model with a MATF card for instance.

