MV-9003:LuGre摩擦のチュートリアル
本チュートリアルでは、新規MotionSolveオブジェクトの実装および使用法を学習します。
- LuGre摩擦モデルを使用し、また、クラスを用いたオブジェクト指向設計を使用して、並進ジョイントに摩擦力を作成します。
クラスとは、より高レベルのエンティティを作成し、それを他のMotionSolveオブジェクトと同じように扱うことができる青写真、またはテンプレートのことです。
この例では、一連のMotionSolveエンティティをLuGreというクラスに結合し、新しい挙動を示す新規モデリング要素を定義します。この処理は集約と呼ばれ、MotionSolveはそのようなオブジェクトを表現するための特別なCompositeクラスを提供します。
Composite(複合)は、パート、マーカー、フォース、微分方程式、その他のMotionSolveプリミティブなどのエンティティを集約することを可能にする特別なクラスです。Compositeクラスオブジェクトは他のソルバーオブジェクトと同じように動作しますが、扱いやすいようにまとめてパッケージ化されたエンティティの集合という点が異なります。これらのオブジェクトはアトミックエンティティとして動作するため、複数回インスタンス化できます。
複合クラスを使う利点は、LuGreオブジェクトが基底クラスから動作を継承することです。特に、パートやマーカーなどの他のMotionSolveプリミティブオブジェクトに対して modify コマンドを発行するのと同じように、実行時にLuGreオブジェクトを修正することができます。次の例では、独自の複合クラスを作成する方法を示します。はじめに、LuGre摩擦モデルを検証します。
LuGre摩擦モデル
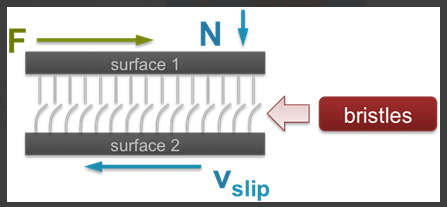
- = 静摩擦から動摩擦への遷移速度
- = 静摩擦係数
- = 動摩擦係数
- = ブリスル剛性
- = ブリスル減衰
- = 粘性係数
- ジョイント内の速度 v =
- ストライベック係数
- 垂直抗力
- クーロン摩擦
- 静摩擦
- ブリスルたわみzを定義する常微分方程式
- 摩擦力
- ブリスルたわみを定義するDIFF
- 摩擦力の作用点を定義するMARKER
- 摩擦力を定義するFORCE
- ブロック上の摩擦力を取り込むREQUEST
msolveモジュールの読み込み
-
msolveモジュールを読み込むには、以下のコマンドを実行します:
In [1]: from msolve import*上記のコマンドを実行するには、msolveモジュールがコンピュータのパスになければなりません。上記が成功したと仮定すると、msolveの名称は現在のネームスペースにインポートされています。これにより、msolveで定義されているすべてのクラスと関数にアクセスできるようになり、LuGreクラスの作成とモデルのサポートを開始することができます。
以下に、このクラスの全体の実装を示します。各セクションは、コードセルに続く段落で確認されます。In [2]: # Create a LuGre Composite Class class LuGre(Composite): joint = Reference (Joint) vs = Double (1.E-3) mus = Double (0.3) mud = Double (0.2) k0 = Double (1e5) k1 = Double (math.sqrt(1e5)) k2 = Double (0.4) def createChildren (self): """This is called when the object is created so the children objects """ # The DIFF defining bristle deflection self.diff = Diff(routine=self.lugre_diff, ic=[0,0]) # The MARKER on which the friction force acts self.im = Marker() # The FORCE defining the friction force self.friction = Sforce (type="TRANSLATION", actiononly = True, routine = self.lugre_force, ) # The REQUEST capturing the friction force self.request = Request (type="FORCE", comment="Friction force") def updateChildren(self): # Set topology self.friction.i =self.joint.iself.friction.j =self.joint.jself.im.setValues (body=self.joint.i.body, qp=self.joint.i.qp, zp=self.joint.i.zp) self.request.setValues (i=self.im, j=self.joint.j, rm=self.joint.j) def validateSelf(self, validator): validator.checkGe0 ("vs") validator.checkGe0 ("mus") validator.checkGe0 ("mud") validator.checkGe0 ("k0") validator.checkGe0 ("k1") validator.checkGe0 ("k2") if self.mud > self.mus: msg = tr("Mu dynamic({0}) needs to be smaller than Mu static ({1})", self.mud,self.mus) validator.sendError(msg) -
クラスが定義されたので、実装の詳細を記入する必要があります。LuGre摩擦は、2つのボディ間の単一成分の力と、滑り速度、摩擦係数、および法線力の関数としてブリスルの平均たわみをモデル化する1次微分方程式を使用しています。まずは単一成分の力に取り組みます。Sforce関数(通常はSfoSubと呼ばれる)の目的は、摩擦力のスカラー値を計算して返すことです。ここで描かれている3つの成分は、力関数の中で別々に計算されます。
def lugre_diff(self, id, time, par, npar, dflag, iflag): "Diff user function" i = self.joint.i j = self.joint.j vs = self.vs mus = self.mus mud = self.mud k0 = self.k0 z = DIF(self) v = VZ(i,j,j,j) N = math.sqrt (FX(i,j,j)**2 + FY(i,j,j)**2) fs = mus*N fc = mud*N p = -(v/vs)**2 g = (fc + (fs - fc) * math.exp(p))/k0 def smooth_fabs(x): returnmath.fabs(x) # temp solution if iflag or math.fabs(g) <1e-8: return v else: return v - smooth_fabs(v) * z / g def lugre_force (self,id, time, par, npar, dflag, iflag): "Friction Force user function" i = self.joint.i j = self.joint.j diff = self.diff k0 = self.k0 k1 = self.k1 k2 = self.k2 v = VZ(i,j,j,j) z = DIF(diff) zdot = DIF1(diff) F = k0*z + k1*zdot + k2*v #print "Time=", time, " V=", v, " Z=", z, " ZDOT=", zdot, " F=", F #print "k0*z=", k0*z, " k1*zdot=", k1*zdot, " k2*v=", k2*v return -F複合クラスLuGreは、組み込みの複合クラスから継承されます。2つの特別なメソッドcreateChildrenおよびsetChildDataValueを記述して、このクラスの挙動を定義する必要があります。オプションとして検証メソッドvalidateSelfを記述することもできます。
各複合クラスには2つのメソッドが必要です。- 1つ目のメソッドは、createChildrenと呼ばれます。このメソッドは、その複合クラスで必要なすべてのMotionSolveエンティティを作成するために使用されます。複合クラスオブジェクトが作成されると、createChildrenメソッドが呼び出されます。この呼び出しは、複合オブジェクトの作成時に一度だけ行われます。createChildren内で、さまざまなMotionSolveオブジェクトをインスタンス化し、これらのオブジェクトの不変のプロパティを定義します。
- updateChildrenメソッドは、クラスのすべての変更可能なプロパティを定義し、新しい値でクラスオブジェクトを更新するために使用されます。これにより、ソルバーが実行されているときに、他のMotionSolveプリミティブオブジェクトと同様に、実行時に値を変更することが容易になります。これについては、チュートリアルで後ほど詳しく説明します。
validateSelfというオプションのメソッドを定義することができます。このメソッドは、入力をチェックして、LuGreクラスに渡されたデータが物理的に意味があることを確認します。例えば、静摩擦係数が動摩擦係数よりも大きいことを検証することで、それを確認することができます。
上記の方法の後には、2つの機能が追加されます。それらは、SforceおよびDiffユーザーサブルーチンです。これらの関数は、クラス定義内で直接作成されることにご留意ください。これを行うメリットは、クラスのプロパティをサブルーチンの実装で利用できるようにすることです。
これにより、ユーザのサブルーチンにパラメータを渡す必要がなくなります。
Sforceサブルーチンは、下の画像で示すように、摩擦Sforceの3つの成分を計算します。図 2. 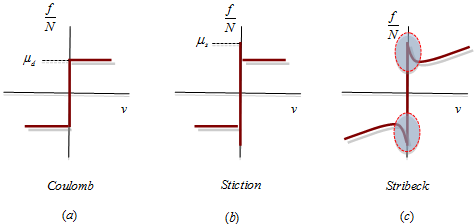
SforceおよびDiffユーザーサブルーチンは、Python の呼び出し可能なクラスメソッドなので、関数の第1引数はselfです。また、Sforce関数の署名はおなじみの形式(id、par、nparなど)になっていますが、サブルーチンに何も渡す必要がないので、実際にはパラメータを解凍していないことにも注意が必要です。
実際には、インスタンス自体にドット演算子を使用してLuGreインスタンスのプロパティにアクセスしています。
同様に、微分方程式を定義することもできます。これはまた、LuGreプロパティに直接アクセスします。
モデルの作成
これでLuGreクラスを完全に定義し、SforceとDiffの2つのメソッド を実装したので、テストに適したモデルを作成する必要があります。
滑りブロック上の2つのボディ間に定義された単純な摩擦要素を使用することができます。滑りブロックは並進ジョイントによって拘束され、強制機能が作用します。
静的摩擦係数μsを変更することで、計算された摩擦力に与える影響をシミュレーション間で修正して検討することができます。
モデルは、以下のコードセル内の_slidingblockという関数の中に作成されます。これは純粋に便宜上行われます。
-
このコマンドを実行します:
In [2]: ################################################################################ # Model definition # ################################################################################ def sliding_block (): """Test case for the LuGre friction model Slide a block across a surface. The block is attached to ground with a translational joint that has LuGre friction """ model = Model () Units (mass="KILOGRAM", length="METER", time="SECOND", force="NEWTON") Accgrav (jgrav=-9.800) Integrator (error=1e-5) Output (reqsave=True) # Location for Part cm and markers used for the joint markers qp = Point (10,0,0) xp = Point (10,1,0) zp = Point (11,0,0) ground = Part (ground=True) ground.jm = Marker (part=ground, qp=qp, zp=zp, xp=xp, label="Joint Marker") block = Part (mass=1, ip=[1e3,1e3,1e3], label="Block") block.cm = Marker (part=block, qp=qp, zp=zp, xp=xp, label="Block CM") # Attach the block to ground joint = Joint ( type="TRANSLATIONAL", i = block.cm, j = ground.jm, ) # Apply the LuGre friction to the joint model.lugre = LuGre (joint=joint) # Push the block Sforce ( type="TRANSLATION", actiononly =True, i = block.cm, j = ground.jm, function ="3*sin(2*pi*time)", label ="Actuation Force", ) # Request the DISPLACEMENT, VELOCITY and FORCE of the Joint model.r1 = Request ( type ="DISPLACEMENT", i = block.cm, j = ground.jm, rm = ground.jm, comment ="Joint displacement", ) model.r2 = Request ( type="VELOCITY", i = block.cm, j = ground.jm, rm = ground.jm, comment ="Joint velocity", ) model.r3 = Request ( type="FORCE", i = block.cm, j = ground.jm, rm = ground.jm, comment ="Joint force", ) return modelLuGre摩擦の作成は、1つの単一行を呼び出すことで行われます:model.lugre = LuGre (joint=joint)必要なのは、並進ジョイント jointをLuGreクラスのインスタンスに渡すことだけです。
摩擦力の計算に使用されるすべてのプロパティは、クラスインターフェースで定義された値がデフォルトです。もちろん、LuGreクラスに異なる値を渡すこともできますが、今のところはデフォルト値を使用します。
-
モデルをテストし、結果をプロットします。
これで、一連のリクエストを持つ実行コンテナができたので、摩擦力の大きさ、ブロック速度、時間の関数としての変位など、関連するチャンネルのいくつかを選択的にプロットすることができます。
-
プロッティングパッケージをインポートします:
# this line causes the plots to be inlined on this web page %matplotlib inline import matplotlib.pyplot as plt -
続いて、プロットするデータの一部を抽出します。この時点で、プロットオブジェクトを作成して、3つの別々のカーブを表示することが可能です。
- 摩擦力
- ブロックの速度
- ブロックの変位
def plot(model):# get the channels from the model... disp = run.getObject (model.r1) velo = run.getObject (model.r3) force = run.getObject (model.r2) plt.subplot(3, 1, 1) plt.plot(force.times, force.getComponent (3)) plt.title('Friction force') plt.ylabel('force [N]') plt.subplot(3, 1, 2) plt.plot(velo.times, velo.getComponent (3),'r') plt.title('Block Velocity') plt.ylabel('velocity [m/s]') plt.subplot(3, 1, 3) plt.plot(disp.times, disp.getComponent (3),'g') plt.title('Block Displacement') plt.xlabel('time (s)') plt.ylabel('travel [m]') plt.grid(True) plt.tight_layout() # Show the plot plt.show()In [7]: plot(model)図 3. 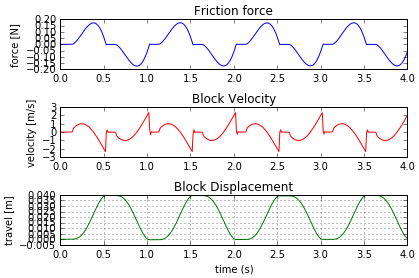
-
摩擦静的係数を大きくするには、LuGre
を別の値に変更し、さらに4秒間シミュレーションを続けます。
In [8]: model.lugre.mus= 0.4 run = model.simulate (type="DYNAMICS", returnResults=True, duration=4, dtout=.01) # replot the quantities and observe the changes to the Friction Force plot(model)図 4. 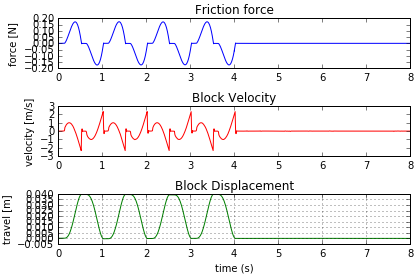
を大きくしたことで、強制関数がブリッスルの抵抗に打ち勝つことができず、ブロックを動かすことができないことがわかります。