PBEND

Bulk Data Entry Defines the property of curved beam or pipe elements defined via the CBEND entry.

Format


(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
PBEND	`PID`	`MID`	`FSI`	`RM`	`T`	`P`	`RB`	`THETAB`
			`NSM`

Example


(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
PBEND	1	2	1	0.85	0.025	50	6.0

Definitions


Field	Contents	SI Unit Example
`PID`	Unique bend property identification. Integer Specifies an identification number for this property. <String> Specifies a user-defined string label for this property. Default = EID (Integer > 0 or <String>)
`MID`	Material identification. 1 Integer Specifies a material identification number. <String> Specifies a user-defined material identification string. 2
`FSI`	Flexibility and stress intensification factors flag. 3 (1≤ Integer ≤ 4)
`RM`	Mean radius of the pipe cross-section. Figure 1 (Real > 0.0)
`T`	Thickness of the wall of the curved pipe. Figure 1 (Real ≥ 0.0; RM + T/2 < RB)
`P`	Internal pressure. (Real or Blank)
`RB`	Radius of the arc of the CBEND element. Required only for `GEOM` = 3 on CBEND. (Real)
`THETAB`	Angle of the arc of the CBEND element. Required only for `GEOM` = 4 on CBEND. (Real, in degrees)
`NSM`	Nonstructural mass per unit length. Default = 0.0 (Real)

Comments

For structural problems, MID may reference only a MAT1 material entry. Only structural problems are currently supported. Heat transfer analysis is not supported for the CBEND/PBEND entries.
String-based labels allow for easier visual identification of properties, including when being referenced by other cards (for example, the PID field of elements). For more details, refer to String Label Based Input File in the Bulk Data Input File topic.

For this Curved Pipe format, the FSI option defines the in-plane flexibility factor (K_z), the out-of-plane flexibility factor (K_y), the in-plane stress intensification factor (S_z), and the out-of-plane stress intensification factor (S_y). K_z and K_y must not be less than 1.0. Accordingly, OptiStruct sets their values to 1.0, when required. The available options are:

FSI = 1


In-plane Flexibility	$K_{z} = 1.0$
Out-of-plane Flexibility	$K_{y} = 1.0$
In-plane Stress	$S_{z} = \frac{I}{A \cdot R_{B}} (\frac{1}{r_{o u t}} + \frac{R_{B} - Δ N}{Δ N \cdot (R_{B} + r_{o u t})})$
Out-of-plane Stress	$S_{y} = 1.0$

Where,

r_{o u t} = R_{M} + \frac{T}{2}

r_{i n} = R_{M} - \frac{T}{2}

I = \frac{1}{4} π (r_{o u t}^{4} - r_{i n}^{4})

A = 2 π \cdot R_{M} \cdot T

A_{m} = 2 π (\sqrt{R_{B}^{2} - r_{i n}^{2}} - \sqrt{R_{B}^{2} - r_{o u t}^{2}})

Δ N = R_{B} - \frac{A}{A_{m}}

Δ N

is the radial offset of the neutral axis due to bending of the curved beam (Boresi, Arthur P., and Richard J. Schmidt. Advanced mechanics of materials. John Wiley & Sons, 2002.)

Figure 1. CBEND Element Coordinate System for Pipe Bend Format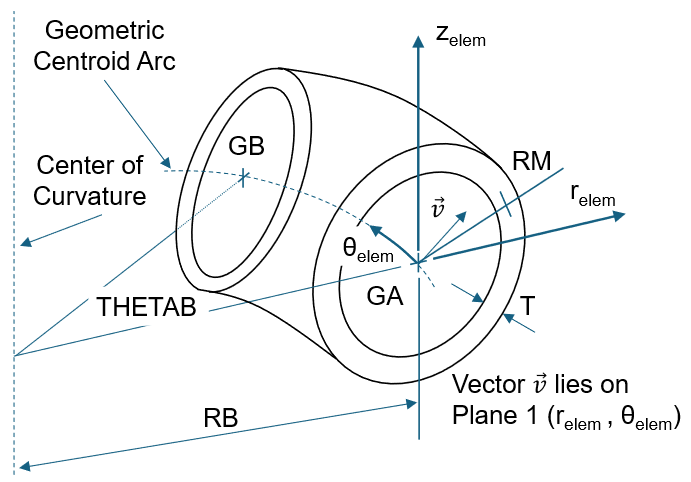

FSI = 2 (ASME code Section III, NB-3687.2, NB-3685.2., 1977)


In-plane Flexibility	$K_{z} = \frac{1.65 R_{M}^{2}}{R_{B} T} (\frac{1}{1 + 6 \frac{P \cdot R_{M}}{E \cdot T} {(\frac{R_{M}}{T})}^{\frac{4}{3}} {(\frac{R_{B}}{R_{M}})}^{\frac{1}{3}}})$
Out-of-plane Flexibility	$K_{y} = K_{z} = \frac{1.65 R_{M}^{2}}{R_{B} \cdot T} (\frac{1}{1 + 6 \frac{P \cdot R_{M}}{E \cdot T} {(\frac{R_{M}}{T})}^{\frac{4}{3}} {(\frac{R_{B}}{R_{M}})}^{\frac{1}{3}}})$
In-plane Stress	$S_{z} = \sin φ + \frac{(1.5 X_{2} - 18.75) \sin 3 φ + 11.25 \sin 5 φ}{X_{4}} + \frac{ν λ (9 X_{2} \cos 2 φ + 225 \cos 4 φ)}{X_{4}}$
Out-of-plane Stress	$S_{y} = \cos φ + \frac{(1.5 X_{2} - 18.75) \cos 3 φ + 11.25 \cos 5 φ}{X_{4}} - \frac{ν λ (9 X_{2} \sin 2 φ + 225 \sin 4 φ)}{X_{4}}$

Where,

λ = \frac{R_{B} \cdot T}{R_{M}^{2} \sqrt{1 - ν^{2}}}

Ψ = \frac{P \cdot R_{B}^{2}}{E \cdot R_{M} \cdot T}

X_{1} = 5 + 6 λ^{2} + 24 Ψ

X_{2} = 17 + 600 λ^{2} + 480 Ψ

X_{3} = X_{1} X_{2} - 6.25

X_{4} = (1 - ν^{2}) (X_{3} - 4.5 X_{2})

With

φ = 0^{o}, 90^{o}, 180^{o}, 270^{o}

corresponding to the default stress recovery points, Di, Ci, Fi, Ei, respectively (Figure 1).

Note: The above equations are only valid for

λ \geq 0.2

, as per NB-3685.1. For ,

λ < 0.2

, a warning is issued but the solution sequence is not interrupted.

FSI = 3 (Research Council Bulletin 179, Dodge and Moore)


In-plane Flexibility	$K_{z} = \frac{1.73}{λ} (\frac{1}{1 + 1.75 λ^{- \frac{4}{3}} \exp (- 1.15 Ψ^{- \frac{1}{4}})})$
Out-of-plane Flexibility	$K_{y} = K_{z} = \frac{1.73}{λ} (\frac{1}{1 + 1.75 λ^{- \frac{4}{3}} \exp (- 1.15 Ψ^{- \frac{1}{4}})})$
In-plane Stress	$S_{z} = \frac{2 λ^{- \frac{2}{3}} (1 + 0.25 {(\frac{R_{B}}{R_{M}})}^{- 1})}{1 + λ^{- \frac{4}{3}} \exp (- Ψ^{- \frac{1}{4}})}$
Out-of-plane Stress	$S_{y} = S_{z} = \frac{2 λ^{- \frac{2}{3}} (1 + 0.25 {(\frac{R_{B}}{R_{M}})}^{- 1})}{1 + λ^{- \frac{4}{3}} \exp (- Ψ^{- \frac{1}{4}})}$

Where $λ$ and $Ψ$ are defined as in FSI = 2.

FSI = 4 (ASME code N-319-3 (approval date of January 17, 2000))


In-plane Flexibility	THETAB = 0°: $K_{z} = 1.0 (\frac{1}{1 + \frac{P \cdot R_{M} \cdot Χ_{Κ}}{T \cdot E}})$ THETAB = 45°: $K_{z} = \frac{1.10 R_{M}^{2}}{T \cdot R_{B}} (\frac{1}{1 + \frac{P \cdot R_{M} \cdot Χ_{Κ}}{T \cdot E}})$ THETAB = 90°: $K_{z} = \frac{1.30 R_{M}^{2}}{T \cdot R_{B}} (\frac{1}{1 + \frac{P \cdot R_{M} \cdot Χ_{Κ}}{T \cdot E}})$ THETAB ≥ 180°: $K_{z} = \frac{1.65 R_{M}^{2}}{T \cdot R_{B}} (\frac{1}{1 + \frac{P \cdot R_{M} \cdot Χ_{Κ}}{T \cdot E}})$ Where, $Χ_{Κ} = 6 \cdot {(\frac{R_{M}}{T})}^{\frac{4}{3}} {(\frac{R_{B}}{R_{M}})}^{\frac{1}{3}}$ For any values 0° < THETAB < 180°, $K_{z}$ is linearly interpolated with THETAB. The resulting $K_{z}$ must not be less than 1.0.
Out-of-plane Flexibility	$K_{y} = \frac{1.25 R_{M}^{2}}{T \cdot R_{B}} (\frac{1}{1 + \frac{P R_{M}}{T \cdot E \cdot Χ_{Κ}}})$
In-plane Stress	THETAB = 0°: $S_{z} = 1.0$ THETAB = 45°: $S_{z} = \frac{1.75}{{(\frac{T \cdot R_{B}}{R_{M}^{2}})}^{0.56}}$ THETAB ≥ 90°: $S_{z} = \frac{1.95}{{(\frac{T \cdot R_{B}}{R_{M}^{2}})}^{2 / 3}}$ For any values 0° < THETAB < 90° , $S_{z}$ is linearly interpolated with THETAB. The resulting $S_{z}$ must not be less than 1.0 or the interpolated value for THETAB = 30° . OptiStruct modifies the value of accordingly.
Out-of-plane Stress	$S_{y} = \frac{1.71}{{(\frac{T \cdot R_{B}}{R_{M}^{2}})}^{0.53}}$ The resulting $S_{y}$ must not be less than 1.0. OptiStruct modifies the value of accordingly.

The stress intensification factors, which determine the stresses at the two endpoints of the CBEND elements, are by default at the stress recovery points Ci, Di, Ei, Fi (i = 1,2 corresponding to grid points A and B) of the cross section (Figure 2).
Figure 2. Default Stress Recovery Points at Cross Section of CBEND Element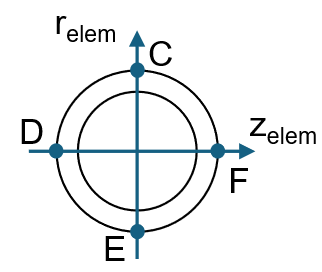
For this curved pipe format of the PBEND card, the shear effects in the stiffness matrix are considered via the following shear correction factor:
$K = \frac{0.75}{1 + \frac{q}{1 + q^{2}}}$
Where, $q = r_{i n} / r_{o u t}$ .