MATS1

このエントリは、非線形サブケースにおいて同じMIDでMAT1エントリが指定された場合に使用されます。

フォーマットA（HR = 1または3）

例A（HR = 1、2、3）

フォーマットB.1（HR = 6：移動硬化（NLKIN）、TYPKIN=PARAM）

フォーマットB.2（HR = 6：移動硬化（NLKIN）、TYPKIN=HALFCYCL）

フォーマットB.3（HR = 6：等方硬化（NLISO）、TYPISO=PARAM）

フォーマットB.4（HR = 6：等方硬化（NLISO）、TYPISO=TABLE）

例（HR = 6）：移動硬化

例（HR = 6）：複合硬化

TYPKIN=PARAM、NLKIN=2、温度依存

例（HR = 6）：移動硬化

定義

コメント

1. 文字列ベースのラベルは、他のエントリ（プロパティのMIDフィールドなど）により参照される場合などに視認をより迅速にします。詳細については、文字列ラベルベースの入力ファイルをご参照ください。
2. 弾塑性材料の場合、弾性応力-ひずみマトリックスはMAT1エントリから計算され、等方性塑性理論を使用して塑性解析が実行されます。

   表ID TIDまたは加工硬化勾配Hのいずれかを指定できますが、両方は指定できません。

3. TIDが指定されている場合、応力 - ひずみデータ（ $\text{ε}$ _x,Y_x）に関するTABLES1、TABLEG、TABLEST、またはTABLEMDエントリ（Xi,Yi）は、以下に従う必要があります：

   エンティティ	TYPE = PLASTIC
   象限	塑性応力-ひずみ曲線は、第1象限のみで定義する必要があります。
   最初のポイント	TYPSTRN = 0の場合、 最初のポイントは原点（X1 = 0、Y1 = 0）である必要があります。 2番目のポイント（X2、Y2）は、初期降伏ひずみ（X2=LIMIT1/E）における初期降伏応力（Y2=LIMIT1）である必要があります。 原点と初期降伏応力を結ぶ線の勾配は、Eの値と等しい必要があります。 TYPSTRN = 1の場合、 最初のポイント（X1、Y1）は相当塑性ひずみが0（X1=0）の初期降伏応力（Y1=LIMIT1）に対応します。
   その他の詳細	データポイントは昇順に指定する必要があります。 TYPSTRN = 1の場合、 TIDによってTABLESTエントリを参照することが可能です。 その場合、TABLES1が指し示すすべてのTABLEST表に上記規則が適用されます。

   • 微小変形の場合、真の応力-ひずみ曲線と工学応力-ひずみ曲線がほとんど同じなため、どちらも表定義に使用できます。
   • 大変形の場合は、真の応力-ひずみ曲線を使用する必要があります。
   • 変形が表で定義されている値を超えている場合、線形外挿が行われます。
4. TIDがTABLEMDを参照している場合、以下が適用されます：

   Xi_j	陰解法解析（SMDISP/LGDISPのNLSTAT / 非線形過渡解析）	陽解法解析
   Xi_1	相当塑性ひずみこれは、速度依存と非依存の両方の問題で使用できます。	速度非依存の問題の場合、塑性ひずみまたは全ひずみを表します。
   Xi_2	速度依存の問題の場合、塑性ひずみ速度を表します。 X2の1つの値のみが指定された場合は、速度非依存のままです。	速度依存の問題の場合、塑性ひずみ速度または全ひずみ速度を表します。
   Xi_3	温度	N/A

5. 速度依存塑性に関する情報：

   エンティティ	陰解法解析（SMDISP/LGDISPのNLSTAT / 非線形過渡解析）	陽解法解析
   アクティブ化	速度依存塑性は、TIDフィールドでTABLEMD IDを指定することによってアクティブにできます。この場合、区分線形関数が使用されます。	速度依存塑性は、複数の方法でアクティブにできます。 TIDフィールドでTABLEMD IDを指定します。この場合、区分線形関数が使用されます。 Johnson-Cookモデル（ひずみ速度がRSTRTより大きい場合のみ）。 クラッシャブルフォームモデル。 Cowper-Symondsモデル。
   要素	ソリッド要素のみ。	シェルおよびソリッド要素。
   温度依存速度依存塑性	サポート。温度依存は、TIDフィールドを介してTABLESTエントリを参照することで定義されます。	未サポート。
   TABLEMD定義	TABLEMDでは、以下を表す最大4つのフィールドを使用できます。 降伏応力 Equivalent plastic strain 塑性ひずみ速度 温度 現時点では、実験データのみ使用できます。塑性ひずみ速度が0の応力-ひずみ曲線を提供する必要があります。	TABLEMDでは、以下を表す最大3つのフィールドを使用できます。 降伏応力 Equivalent plastic strain 塑性/全/体積ひずみ速度
   サポートされているひずみ速度	塑性ひずみ速度のみがサポートされています。そのため、全ひずみ速度入力（TYPSTRT=0）は無視されます。	塑性/全/体積ひずみ速度がサポートされています。
   その他の注意	全ひずみ入力（TYPSTRN=0）はサポートされておらず、無視されます。 TABLEMDの2列目は相当塑性ひずみにする必要があります。

   混合硬化（HR=1、2、3、または実数値）は、速度依存塑性（TID=TABLEMD）と組み合わせることができます。

6. 移動硬化と混合硬化のサポート情報は次のとおりです：

   サポートされるエンティティ	陰解法解析（NLSTATと非線形過渡解析）	陽解法解析
   要素	SMDISP シェル（1次）要素とソリッド要素 LGDISP シェル（1次）要素とソリッド要素	シェル要素とソリッド要素

7. 応力対全ひずみ（TYPSTRN=0）から応力対塑性ひずみ（TYPSTRN=1）の変換の関係をFigure 1に示します。これは、全部の表をひずみの軸に沿って単純にシフトしたのとは明らかに異なります。

   
   
   

8. MATS1の要素サポート制限：

   要素タイプ

   制限事項

   2次シェル要素（CTRIA6とCQUAD8）

   • MATS1はサポートされていません。

   CROD、CONROD、CBAR、およびCBEAM

   • MATS1は、軸並進方向でのみサポートされています
   • 他の方向の挙動は弾性が維持されます。具体的には、CROD/CONROD要素のねじれ変形、またはCBAR/CBEAM要素のせん断変形、曲げ変形、およびねじれ変形では弾性が維持されます。

9. Johnson-Cookモデルに関する情報：

   エンティティ

   詳細

   解析タイプ

   陽解法動解析でのみサポートされています。

   ひずみ速度依存

   ひずみ速度が参照ひずみ速度を上回っている場合のみアクティブになります。

   定式化：
   $$\sigma =\left(a+b{\epsilon }_p^n\right)\left(1+c\ln \left(\frac{\dot{\epsilon }}{{\dot{\epsilon }}_0}\right)\right)$$
   $$\overline{\sigma }=\left(A+B{\left({\overline{\epsilon }}^{pl}\right)}^n\right)\left(1+C\ln \left(\frac{{\dot{\overline{\epsilon }}}^{pl}}{{\dot{\epsilon }}_0}\right)\right)$$

   Johnson-Cookひずみ速度依存では、以下のように見なされます：

   $$\overline{\sigma }={\sigma }^0\left({\overline{\epsilon }}^{pl},\theta \right)R\left({\dot{\overline{\epsilon }}}^{pl}\right)$$

   かつ ${\dot{\overline{\epsilon }}}^{pl}={\dot{\epsilon }}_0\exp \left(\frac{1}{C}\left(R-1\right)\right)$ （ $\overline{\sigma }\ge {\sigma }^0$ の場合）

   ここで、

   $\overline{\sigma }$

   ゼロ以外のひずみ速度での降伏応力

   ${\overline{\epsilon }}^{pl}$

   相当塑性ひずみ

   ${\dot{\epsilon }}_0$ および $C$

   遷移温度以下で測定した材料パラメータ ${\theta }_{transition}$

   ${\sigma }^0\left({\overline{\epsilon }}^{pl},\theta \right)$

   静的降伏応力

   $R\left({\dot{\overline{\epsilon }}}^{pl}\right)$

   静的降伏応力に対するゼロ以外のひずみ速度での降伏応力の比率 $R\left({\dot{\epsilon }}_0\right)=1.0$

10. クラッシャブルフォームモデルに関する情報：

    エンティティ

    詳細

    解析タイプ

    陽解法動解析でのみサポートされています。

    TSC定義

    引張荷重下にあるクラッシャブルフォームの降伏応力を示す正の応力値として定義されます。

    表定義

    圧縮荷重下にあるクラッシャブルフォームの降伏応力は、以下のルールが適用される速度非依存の表（TABLES1）で得られます：

    • 表のx値は体積ひずみです（すべての正の値は体積が圧縮されていることを示します）。体積ひずみは $\gamma =1-\frac{V}{V_0}$ と定義できます。
    • 表のy値は圧縮降伏応力です（すべて正の値）。
      注: クラッシャブルフォームは体積ひずみベースの定義に基づいているため、TYPSTRN = 0（デフォルト）は無効で、TYPSTRN = 1を指定する必要があります。
    • 1番目のエントリはx=0、y=y_0（初期圧縮降伏応力）です。
    • すべてのxiは、昇順とした正の値とする必要があります。

    特定の出力

    相当塑性ひずみの代わりに、積分した体積ひずみ結果（相対体積の自然対数 $-In\left(\frac{V}{V_0}\right)$ ）が出力されます。

11. Cowper-Symondsモデルに関する情報：

    エンティティ

    詳細

    解析タイプ

    陽解法動解析でのみサポートされています。

    TYPSTRT

    全ひずみ速度または塑性ひずみ速度のどちらかを使用できます。

    $f\left({\epsilon }^{pl}\right)$

    TABLES1またはTABLEMDを使用して線形硬化形式または表形式で指定できます。

    定式化：

    降伏応力は次のように計算されます：

    $${\sigma }_y=\beta f\left({\epsilon }^{pl}\right)$$
    ここで、

    $f\left({\epsilon }^{pl}\right)$

    参照速度塑性ひずみ対降伏応力硬化関数。

    $\beta$

    ひずみ速度効果の項。次のように計算されます： $\beta =1+{\left(\frac{\dot{\epsilon }}{D}\right)}^{\frac{1}{p}}$ 。

12. 複合硬化の使用に関する情報：

    エンティティ

    詳細

    解析タイプ

    陰解法解析（SMDISP/LGDISPの非線形静解析 / 過渡解析）でのみサポートされています。

    要素タイプ

    ソリッド要素でのみサポートされています。

    複合硬化による速度依存塑性

    サポートされていないため、TIDフィールドは無視されます。

    組み合わせの柔軟性

    NLKINとNLISOのどちらも、パラメータ入力または応力-ひずみ曲線入力のどちらかをサポートしています。

    これらは、NLKINとパラメータ入力（PARAM）や、NLISOと応力-ひずみ曲線入力（TABLE）のように柔軟に組み合わせることができます。

    少なくとも1つの非線形硬化のタイプを定義する必要があります。詳細については、von Mises塑性の複合硬化をご参照ください。

13. NLKINまたはNLISOの使用に関する情報：

    エンティティ

    詳細

    解析タイプ

    陰解法解析（SMDISP/LGDISPのNLSTAT / 非線形過渡解析）でのみサポートされています。

    温度依存性

    TYPKIN = HALFCYCLまたはTYPISO = TABLEの場合は、複数の曲線を次々に指定できます。最終列の温度（TEMP）は昇順にする必要があります。TYPKIN/TYPISO = PARAMの場合は、TEMPを昇順で指定して、パラメータを温度依存にすることができます。

    パラメータフィッティング（TABLE/HALFCYCLの場合）

    Levenberg-Marquardtの手法が使用されます。

    パラメータは温度ごとに.outファイルに出力されます。

    相当塑性ひずみの決定

    NLKINでは、通常、実験の最初のサイクルから直接調達されます。NLISOでは、通常、繰り返し荷重実験から調達されます。

    その他の注意

    NLKINとNLISOの両方でPARAMフォーマットが使用されている場合、初期降伏応力SIGY0は同じ温度では同じ値にする必要があります。

    この継続行の後で、無制限の数の継続行をデータブロックに追加できます。

14. TYPKIN=PARAMの場合は、逆応力の数が4以上であれば、複数の継続行を使用してパラメータの完全なセット（C1-C10、G1-G10）を定義できます。上の例をご参照ください。
15. 温度依存材料は、サブケースの種類によって異なるオプション（TEMP(MAT）、TEMP(BOTH）、DLOAD （ TLOAD1, TLOAD2、およびTEMP/TEMPDバルクデータエントリ経由）など.）を使って、サブケースレベルで有効にすることができます。
16. 温度依存材料は、サブケースの種類によって異なるオプション（TEMP（MAT）、TEMP（BOTHDLOAD（TLOAD#およびTEMP/TEMPDバルクデータエントリ経由など））を使って、サブケースレベルでアクティブにすることができます。詳細については、TEMPERATUREサブケース情報エントリのComment 2をご参照ください。
17. 損傷開始および進展の破壊基準は、次の2つの方法で定義できます：
    • MATS1バルクデータエントリのDAMAGE継続行を使用する。この方法は、陰解法動解析と陽解法動解析の両方でサポートされています。
    • MATFバルクデータエントリのCRI=INIEVOを使用します。この方法は、陽解法動解析でのみサポートされています。

    詳細については、ユーザーズガイドの陽解法動解析のセクションでMaterial Failure Criterionをご参照ください。

18. Johnson-Holmquist材料モデルは、脆性材料挙動のモデル化に使用できます。これはMAT1弾性挙動で使用でき、現時点ではソリッド要素でのみサポートされています。せん断係数（ $G$ ）と体積弾性率（ $K_1$ ）を使用して、次のように対応するヤング率とポアソン比を入力できます。
    $$E=\frac{9K_{1}G}{3K_1+G}$$ $$\nu =\frac{3K_1-2G}{6K_1+2G}$$

    相当応力は、正規化されたフォンミーゼス応力です：

    $${\sigma }_{VM}^{*}=\frac{1}{{\sigma }_{HEL}}\sqrt{\frac{3}{2}\left({\sigma }_{xx}^2+{\sigma }_{yy}^2+{\sigma }_{zz}^2+2{\sigma }_{xy}^2+2{\sigma }_{yz}^2+2{\sigma }_{zx}^2\right)}$$
    正規化応力がHugoniot弾性限界である場合、この応力は次のように計算されます：
    $${\sigma }_{HEL}=\frac{3}{2}\left(HEL-P_{HEL}\right)$$

    正規化されたフォンミーゼス応力（ ${\sigma }_{VM}^{*}$ ）は、以下により得られる正規化された降伏応力 ${\sigma }^{*}$ と比較されます。

    $${\sigma }^{*}=\left(1-D\right){\sigma }_i^{*}+D{\sigma }_f^{*}$$

    ここで、

    ${\sigma }_i^{*}$

    未加工の材料降伏応力： ${\sigma }_i^{*}=a{\left(P^{*}+T^{*}\right)}^n\left(1+c\ln \left(\frac{\dot{\epsilon }}{{\dot{\epsilon }}_0}\right)\right)$

    ${\alpha }_f^{*}$

    破壊した材料の降伏応力： ${\sigma }_f^{*}=b{\left(P^{*}\right)}^m\left(1+c\ln \left(\frac{\dot{\epsilon }}{{\dot{\epsilon }}_0}\right)\right)<{\sigma }_{fmax}^{*}$

    ここで、

    $$\sigma *=\frac{\sigma }{{\sigma }_{HEL}}$$

    $$P^{*}=\frac{P}{P_{HEL}}$$

    $$T^{*}=\frac{T}{P_{HEL}}$$

    損傷パラメータが指定されていない場合 $(D_1=D_2=0)$ 、塑性ひずみの進展は計算されず、要素の挙動が弾性限界に達すると即座に破壊が得られます。それ以外の場合、損傷パラメータが記載されていれば、塑性ひずみの進展が計算され、累積損傷が計算されます：

    $$D=\frac{\sum \mathrm{\Delta }{\epsilon }_f^p}{{\epsilon }_f^p}$$

    ここで、破壊する塑性ひずみは次のように計算されます：

    $${\epsilon }_f^p=D_1{\left(P^{*}+T^{*}\right)}^{D_2}$$

    最大圧力引張強度は、損傷時に以下のように低下します：

    $$P^{*}=-\left(1-D\right)T^{*}$$

    これにより、損傷時に ${\sigma }_i^{*}$ と ${\sigma }_f^{*}$ の間の滑らかな遷移が可能になります。

    
    
    

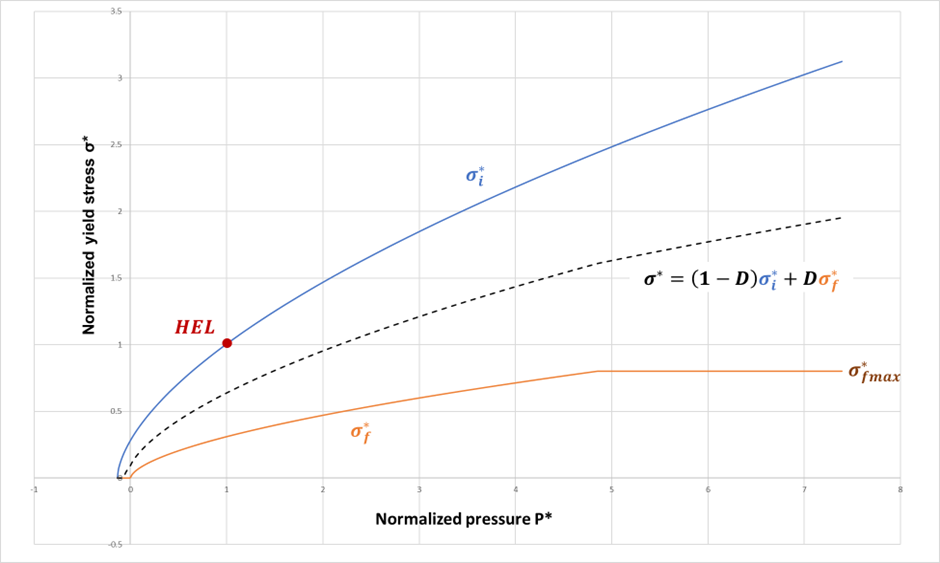
    圧力は次のように定義される状態方程式に従って計算されます：

    $$P=K_1\mu$$
    （引張の場合）
    $$P=K_1\mu +K_2{\mu }^2+K_3{\mu }^3$$
    （圧縮の場合）

    ここで：

    $$\mu =\frac{\rho }{{\rho }_0}-1$$

    損傷が始まると、体積圧力の増分 $\Delta P$ が、弾性エネルギー損失 $\Delta U$ の関数として計算され、内部ポテンシャルエネルギーに変換されます：

    $$\Delta P_{t+\Delta t}=-K_1\mu +\sqrt{{\left(K_1\mu +\Delta P_t\right)}^2+2\beta K_1\Delta U}$$

    ここで、 $U\left(D\right)=\frac{\sigma }{6G}$ と $\Delta U=U\left(D\right)-U\left(D_{n+1}\right)$ 。

    そして、この増分が上記状態方程式に加算されます。

    $$P_{t+\Delta t}=P_t+\Delta P_{t+\Delta t}$$

19. Johnson-Cook、クラッシャブルフォーム、Cowper-Symonds、Johnson-Holmquist材料など、現在陽解法解析でのみサポートされている一部の非線形材料モデルを、陰解法解析サブケースに使用すると、これらの材料の線形弾性部分のみが陰解法解析で考慮されます。該当するWARNINGメッセージも.outファイルに出力されます。
20. Mohr-Coulomb塑性の使用に関する情報：

    エンティティ

    詳細

    解析タイプ

    陰解法解析（SMDISP/LGDISPのNLSTAT/NLTRAN）でのみサポートされています。

    要素タイプ

    ソリッド要素でのみサポートされています。

    温度依存性

    サポートされていないため、TIDフィールドは無視されます。

    Mohr-Coulomb塑性の式は次の通りです：

    $$\tau =c-{\sigma }_n\tan \varphi$$

    ここで、

    $c$

    凝固

    $\varphi$

    摩擦モデル

    降伏関数を主応力空間で表すと、次のようになります：

    $$f={\sigma }_1-{\sigma }_3+\left({\sigma }_1+{\sigma }_3\right)\sin \varphi -2c\cos \varphi \le 0$$
    流動則は次のように表されます：

    $$g={\sigma }_1-{\sigma }_3+\left({\sigma }_1+{\sigma }_3\right)\sin \phi$$

    ここで、

    ${\sigma }_1$

    特定の応力状態の最大主応力

    ${\sigma }_3$

    特定の応力状態の最小主応力

    $\phi$

    ダイラタンシー角

21. Linear Drucker-Prager塑性の使用に関する情報：

    エンティティ

    詳細

    解析タイプ

    陰解法解析（SMDISP/LGDISPの非線形静解析 / 過渡解析）でのみサポートされています。

    要素タイプ

    ソリッド要素でのみサポートされています。

    温度依存性

    サポートされていないため、TIDフィールドは無視されます。

    Linear Drucker-Prager塑性の降伏関数：

    $$f=q+p\tan \beta -d\le 0$$

    流動則は次のように表されます：

    $$g=q+p\tan \phi$$

    LDPの継続行、YIELDフィールドは材料の初期降伏強度を定義し、降伏関数で使用される凝固力dに変換されます。

    TYPE = COMPの場合

    $$d=\left(1-\frac{1}{3}\tan \beta \right){\sigma }_{c0}$$
    およびYIELDは ${\sigma }_{c0}$ を指定します。

    TYPE = TENSの場合

    $$d=\left(1+\frac{1}{3}\tan \beta \right){\sigma }_{t0}$$
    およびYIELDは ${\sigma }_{t0}$ を指定します。

    もしTYPE = COHE, YIELDの場合 $d$ を定義します。

    FRICAとDILAはそれぞれ摩擦角βとダイラタンシー角φを定義します。

22. MC基準からLDP基準への材料定数の変換は、平面ひずみ条件下で次のようにして行います：
    $$\tan \beta =\frac{9\sin \varphi }{\sin \varphi \tan \phi +\sqrt{3\left(9-{\tan }^2\phi \right)}}$$
    $$d=\frac{9c\cos \varphi }{\sin \varphi \tan \phi +\sqrt{3\left(9-{\tan }^2\phi \right)}}$$